and regression for continuous variables. ANCOVA tests whether certain factors have an effect after controlling for quantitative predictors. The inclusion of covariates increases statistical power because it accounts for the variablity.
Equations
One-factor ANCOVA analysis
One factor analysis is appropriate when dealing with more than 3 populations; k populations. The single factor has k levels equal to the k populations. n samples from each population are chosen random from their respective population.Calculating the Sum of Squared Deviates for the Independent Variable X and the Dependent Variable Y
The sum of squared deviates (SS): SSTy, SSTry, and SSEy must be calculated using the following equations for the dependent variable, Y. The SS for the covariate must also be calculated, the two necessary values are SSTx and and SSEx.
The total sum of squares determines the variablility of all the samples. nT represents the total number of samples:
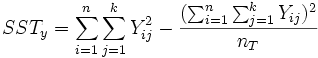
The sum of squares for treatments determines the variablity between populations or factors. nk represents the number of factors:
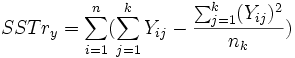
The sum of squares for error determines the variability within each population or factor. nn represents the number of samples with a given population:
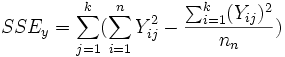
The total sum of squares is equal to the sum of the sum of squares for treatments and the sum of squares for error:
SSTy = SSTry + SSEy
Calculating the Covariance of X and Y
The total sum of square covariates determines the covariance of X and Y within the all the data samples:
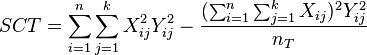
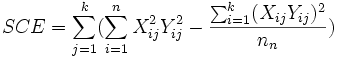
Adjusting the SSTy
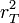 is the correlation between X and Y
is the correlation between X and Y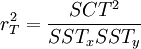
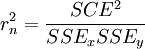
The proportion of covariance is substracted from the dependent, SSy values:
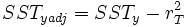

SSTryadj = SSTy[adj] − SSEy[adj]
Adjusting the means of each population k
The mean of each popluation is adjusted in the following manner:
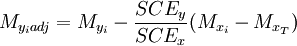
Analysis Using Adjusted Sum of Squares Values
Mean squares for treatments where dfTr is equal to NT − k − 1. dfTr is one less than in ANOVA to account for the convariance and dfE = k − 1:

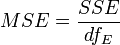
The F statistic
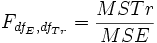
No comments:
Post a Comment